close

- 有內建偏差的樣本
- 抽樣的樣本不足以代表全體,有代表性的樣本,這是指把各種偏差來源都排除的樣本。譬如在街頭或是火車站進行隨機的訪問結果,樣本中會明顯少了總是開車出門的樣本。
- 受訪者想要給一個會讓訪問員喜歡的答案,在閱讀調查結果時,一定要把這點列入考慮。譬如:調差薪資的相關問題時,人們常常會高報薪資或低報薪資,為了虛榮感或是拍被查務考慮。
- 精心選擇的平均
- 當你遇到一個平均工資數字,首先要問的是:這是那些人的平均?
- 有人告訴你某個平均數字的時候,你對它還是所知甚少,除非你知道他們所用的廣義平均,是指平均數,中位數,還是眾數
- 有時數據的分佈情況並非是常態分配(鐘形的兩邊對稱),而會是偏斜的(skewed),外形像是溜滑梯,一端急昇一端緩降,此時平均值會離中位數有點距離,以年收入來統計,如果樣本中少數人的收入遠高於其他人,這樣平均值就會被拉高,而中位數較低,就會出現『幾乎每個人都低於平均』。
- 隱藏起來的小數字
- 不論是平均,圖表,還是上升或下降的趨勢,當重要數字沒有伴隨出現時,你最好別對這些事情認真。
- 取巧之處,是不恰當的樣本,例如取樣數太少,只要樣本數夠小,就會因為機遇而產生出,不代表任何意義的結果。例如:拿一枚硬幣來擲看看正反面的結果,連擲十次後,會是正反面各半嗎?有時候出現八次正面是常見的事。取樣數太少就是有這樣的機率出現特別的結果。那如果連續擲一千次呢?最後就會非常容易接近正反各半。
- 只強調算術平均與中位數,但沒有標示範圍。例如平均溫度都是20度,但是一個地方是10-30度,另一個地方是0到40度,雖然平均值是一樣的,但是變動差很多。
- 建商以家庭平均人數來決定建造房屋時,房間數的參考,例如平均為3.6人,所以規劃了2-3房的方式。但是如果以整體範圍來看,3.6人可能只佔全體的45%,有35%少於3.6人,20%多於3.6人。這樣反而是多數家庭(55%)沒有適合的房型了。
- 庸人自擾篇
- 要考慮IQ分數以及其他許多抽樣結果時,唯一正確的方式,應該要看範圍。
- 抽樣調差時,都會有誤差,例如智力測驗,A 君IQ101與B君IQ98的人,誰比較聰明?要先清楚測驗的誤差有多少,例如誤差值3,那麼A有可能因為誤差而是101-3=98,而 B是98+3=101,因此B君有可能還是比A君聰明的。或是其實兩者差不多
- 如果兩者差異值小於誤差範圍,就沒有排名上的意義了。
- 誇大其辭的圖
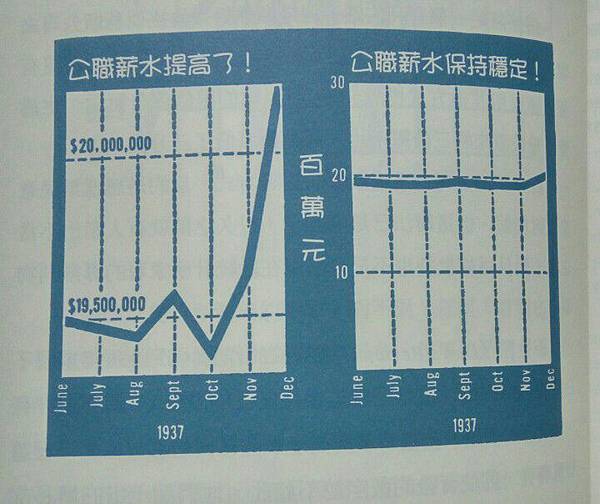
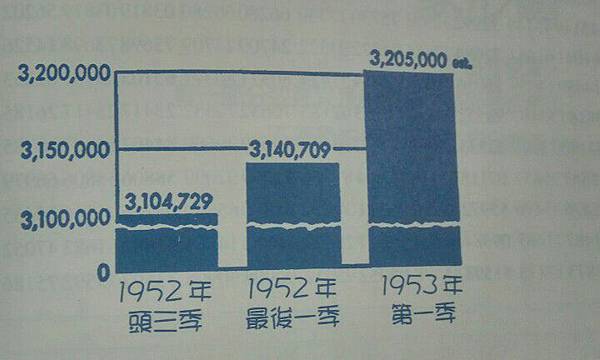
- 新聞週刊在1951年就用這方法呈現了『股票到達21年來的新高』,他們把圖切掉了一部份。
- 改變圖表縱軸與橫軸刻度單位,就可能讓趨勢的感覺改變。
- 象形圖
- 這些現象,有一部份或許只是繪圖者太遜而造成,不過恐拍還是欺騙的成分居多。
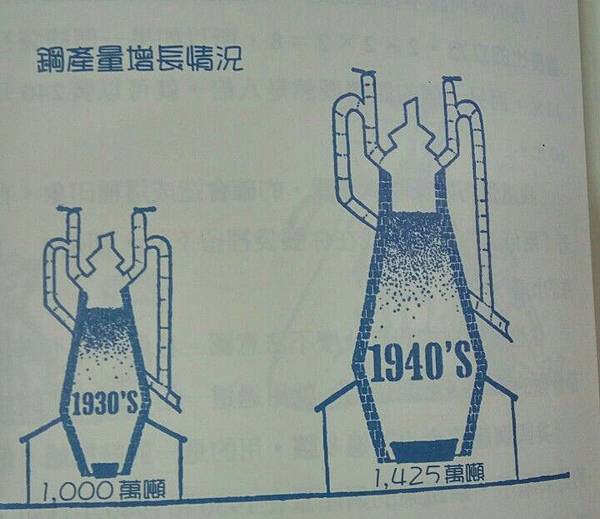
- 以錯誤的圖形比例來誤導,雖然產量增加近50%,但是圖形在寬高各增加50%後,面積是增加了3-4倍的感覺,明顯誤導了結果。
- 似相關而非相關的數字
- 如果你不注意車禍統計數字的實際意義,不論哪種交通工具的統計數字,都可以把你嚇個半死。
- 很大一個樣本的知名醫生當中,有27%抽的是利喉牌香菸。比任何其他牌子都多。除非醫生對於香菸特別有研究,否則這個數據並沒有參考價值。
- 能多榨出26%的果汁的果汁機?如果比較的基礎是手工榨汁,那這臺果汁機跟其它果汁機比較,可能沒有多優秀了。
- 好天氣比有霧的天氣容易出車禍?這是因為有霧的日子太少了。
- 去年因飛機失事而死亡的人數是十年前的1.5倍!所以現在的搭飛機比較危險?其實是現在飛行的班次與人數,比以前多了幾百倍甚至千倍了。
- 你需要清楚的是比例!
- 在美西戰爭中,海軍的死亡率是每千人有九人死亡,而紐約市的老百性是每千人有16人,海軍以此來證明加入海軍是安全的!但是這樣比較是沒有意義的,因為雙方抽樣的樣本條件,根本不一致!
- 『錯亂因果結論』重新出現
- 如果我們會讓統計以及一堆數字與小數點攪亂了因果關係,那麼這比迷信也沒好到哪裡去。
- 統計大學生有抽菸與沒有抽菸的考試成績,結果沒有抽菸的成績較佳,因此推定抽菸對思考有害!這要的假設是有問體題的,或許只是抽菸的人常花比較多的時間在與朋友交際抽菸,所以讀書的時間較少所導致。
- 有高關聯性不一定會有因果關係,有因果關係才會有高關聯性。例如:有天你發現,如果你出門是左轉比起右轉,左轉當天當天股票上漲的機率,高出右轉有兩倍。有高關聯但是不一定有因果!
- 怎樣利用統計來操控
- 如果統計的目的和商業有關,統計學家不太可能去選擇一個不利於結果的方法,就像撰寫廣告詞的人一樣。
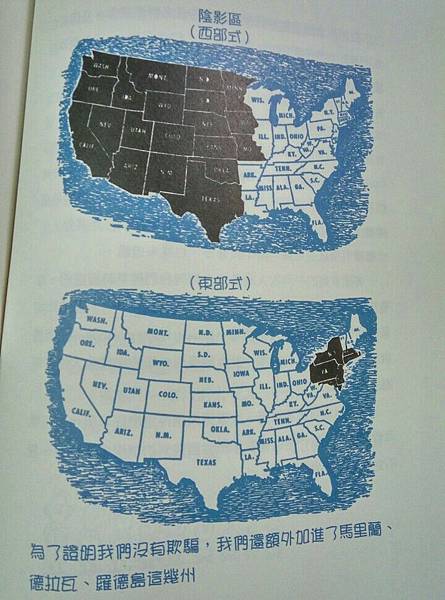
- 利用不同的表示法來誤導,下圖是政府支出佔國民所得的比重,圖上是優先以較低所得與土地面積的州開始塗黑,而下方的條件是以所得高的優先,等是正確的數據,但是印像會差很多。
- 錯誤的計算方式來誤導,例如:公司在去年景氣差時,減薪20%,今年景氣好轉加薪5%,補回了1/4了。這樣的計算是有誤的,實際上如果原本薪資是100元,減薪20%後為80元,加薪5%後為84元,只有恢復1/5!
- 減薪50%之後,要加薪100%才會恢復原本的薪資。
- 利用百分比來誇大效果,工資上升不多,但是利潤上升的很快?換一種表示方法,就完全是不同的效果。公司會說薪資的總金額比利潤高很多,但是要求加薪的員工認為,利潤上升很多,而薪資上升的不高。

- 即使是從是學術研究的人,也可能觀念有所偏差(可能不自覺),或想要證明某個觀點,甚至有所企圖。
- 如何對統計提出質疑
- 碰到有人根據未經證明的假設胡言亂語的時候,只要問一問『這樣有道理嗎?』,就常常可以讓誇大解釋的統計現形。
- 你可以用五個簡單的問題來避勉掉許多不實的訊息。
- 問題一:誰說的?大約第一件該注意的事情,就是有沒有偏差。引用數據的人是否有利益考量?
- 問題二:漏了什麼?在缺乏比較的情況下,很多數字會失去意義。例如有公司的員工數100人,平均分紅是10萬元,其實少數幾個高層主管拿了總分紅的50%,而多數員工分剩下的50%。要注意統計的平均,中位數,眾數,與範圍與比率。缺少的數據可能才是真像。
- 問題四:是否有人改變了主題?要注意從原始數據推導到結論的過程當中,是否有什麼地方被改掉了。例如:應該把住在魔鬼島的囚犯,都送到華爾道夫飯店去住,反而比較省錢。這其實是把監獄的總經費,變成旅館的費用了,如果真要這麼作,除了飯店費用外,還是需要一大比監禁犯人於旅館的管理費用,只會比原本的更高!
- 問題五:這有道理嗎?使用過去的趨勢來預測未來走勢,這其實沒多少意義,除非未來所有的條件都相同,否則跟本不可能照線性發展,例如:銀行股過去十年的殖利率都在5%左右,因此你推定未來十年也會是一樣的結果。這樣的推論是假設未來十年都不會有改變。

全站熱搜
 包子企業.
包子企業.

 留言列表
留言列表